概率论中的互斥事件与相互独立事件是两个基础却极易混淆的概念,它们在游戏设计、算法优化和系统建模中具有广泛应用。本文将从数学定义、几何直观到实际应用,深入剖析这两个核心概念的内在联系与本质区别。
概率论基础:定义与本质
在概率论中,互斥事件和相互独立事件是描述事件关系的两个基本概念。理解这两个概念对于游戏设计中的概率机制构建至关重要。
互斥事件(Mutually Exclusive Events)指的是两个或多个事件不能同时发生。如果事件A和事件B互斥,那么当A发生时,B一定不发生,反之亦然。数学表达式为:
– A ∩ B = ∅(空集)
– P(A ∩ B) = 0
相互独立事件(Independent Events)则是指一个事件的发生不影响另一个事件的发生概率。如果事件A和事件B相互独立,那么:
– P(A ∩ B) = P(A) × P(B)
几何直观:韦恩图解析
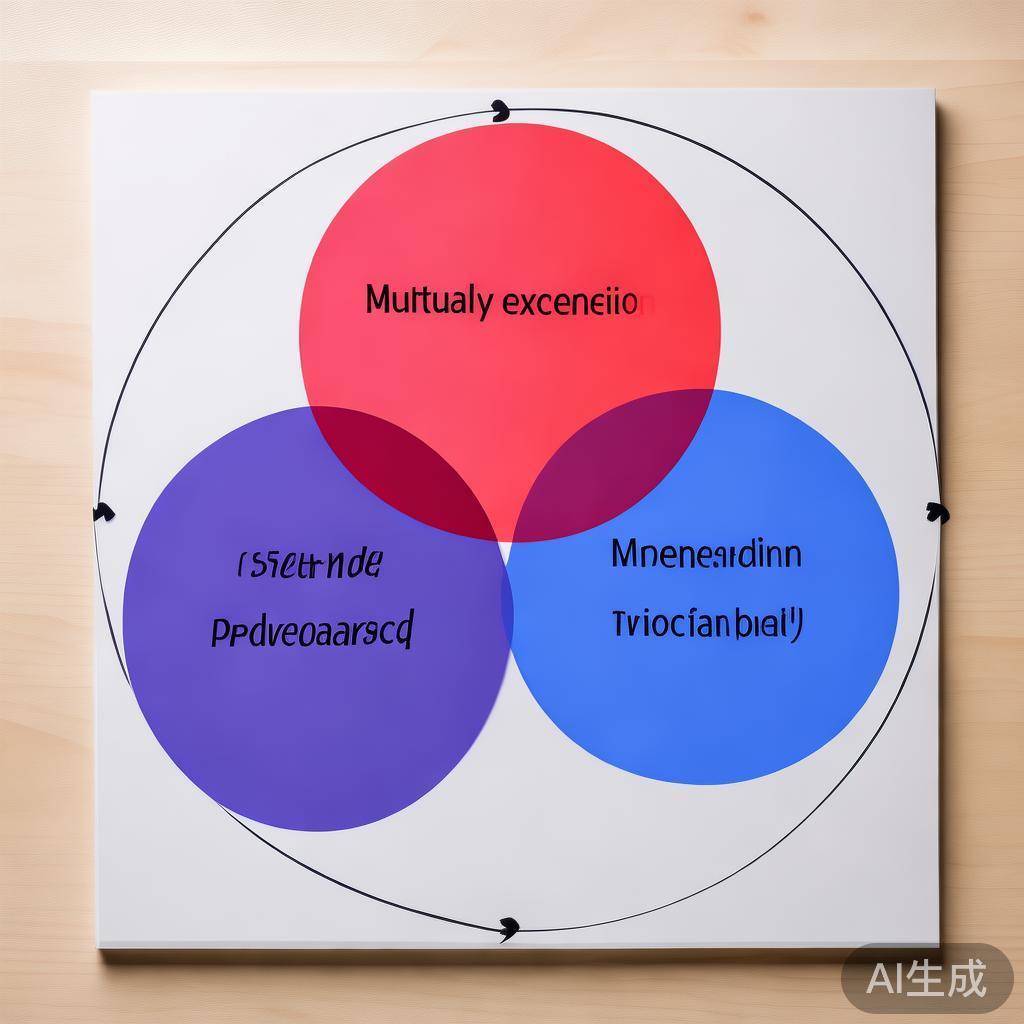
通过韦恩图可以更直观地理解这两个概念:
互斥事件的韦恩图表现为两个完全分离的圆形,没有重叠区域。这直观地表示两个事件不可能同时发生。
相互独立事件的韦恩图则表现为两个有重叠区域的圆形,但重叠区域的大小恰好等于两个事件概率的乘积。这表示两个事件可以同时发生,且它们的交集概率符合独立性的数学定义。
数学关系:互斥与独立的深层联系
互斥事件和相互独立事件之间存在深刻的数学关系:
定理:如果两个事件A和B互斥,且P(A) > 0,P(B) > 0,那么A和B不相互独立。
证明:
– 如果A和B互斥,则P(A ∩ B) = 0
– 如果A和B独立,则P(A ∩ B) = P(A) × P(B)
– 因此,P(A) × P(B) = 0
– 这意味着P(A) = 0或P(B) = 0
这个定理揭示了互斥和独立两个概念在数学上的排他性关系(在非零概率条件下)。
游戏设计理论中的应用
1. 卡牌游戏中的概率机制
在卡牌游戏中,互斥事件的典型应用是:
- 抽卡结果:一次抽卡只能获得一张特定的卡牌,抽到卡牌A就抽不到卡牌B
- 技能触发:在某个时间点只能触发一种技能效果
相互独立事件的应用包括:
- 连续抽卡:每次抽卡的概率都是独立的,前一次结果不影响后一次
- 多重判定:攻击暴击和防御穿透的概率计算相互独立
2. RPG游戏中的属性系统
RPG游戏中的属性系统大量应用了独立事件概念:
- 暴击率和暴伤倍率的计算通常是独立的
- 命中判定和暴击判定分步进行,互不影响
而互斥事件则常见于:
- 装备槽位:同一装备槽位只能装备一件物品
- 技能选择:在技能树中,某些分支路径是互斥的
3. 概率平衡设计
游戏设计师需要深刻理解这两个概念来平衡游戏体验:
- 互斥事件设计:控制玩家选择的多样性,避免过于强大的组合
- 独立事件设计:创造随机性和惊喜感,但需要控制整体期望值
实际案例:概率计算与系统设计
案例1:抽卡系统的概率设计
假设一个抽卡系统:
– 稀有卡概率:5%(互斥事件)
– 普通卡概率:95%(互斥事件)
每次抽卡都是独立事件,前一次抽卡结果不影响后一次。
案例2:战斗系统中的多重判定
战斗系统中的判定通常包含多个独立事件:
– 命中判定:P(命中) = 80%
– 暴击判定:P(暴击) = 20%
– 伤害计算:基于暴击结果独立计算
设计原则与最佳实践
1. 互斥事件设计原则
- 明确边界:清晰定义互斥事件的边界条件
- 平衡选择:确保互斥选项之间的价值相对平衡
- 避免极端:防止某个互斥选项明显优于其他选项
2. 独立事件设计原则
- 控制方差:虽然独立,但需要控制整体概率分布
- 玩家预期:确保随机结果符合玩家的心理预期
- 透明度:向玩家清晰展示概率机制
数学建模与系统优化
在游戏系统的数学建模中,正确区分和使用互斥事件与独立事件至关重要:
1. 期望值计算
对于独立事件系统,期望值计算遵循线性性质:
E[X + Y] = E[X] + E[Y]
对于互斥事件系统,期望值计算需要考虑约束条件。
2. 方差控制
独立事件的方差计算相对简单:
Var(X + Y) = Var(X) + Var(Y)(当X和Y独立时)
而互斥事件的方差控制需要更复杂的约束条件。

结论:理论与实践的统一
互斥事件和相互独立事件是概率论中的基础概念,但它们在游戏设计理论中具有深刻的应用价值。理解这两个概念的本质区别和内在联系,有助于游戏设计师:
- 构建合理的概率系统
- 平衡游戏机制
- 优化用户体验
- 预测玩家行为
通过将数学理论与游戏设计实践相结合,我们可以创造出既符合数学逻辑又具有良好游戏体验的作品。概率论不仅是科学,更是艺术,而游戏设计正是这种艺术的最佳实践领域。
关键词:互斥事件, 相互独立事件, 概率论, 游戏设计, 数学建模, 系统优化, 随机机制, 概率计算, 理论应用
